SPC组态
1.应用场景
统计过程控制(Statistical Process Control,SPC)是品质管理的一种方法,该方法通过自动化监控生产流程中的关键参数(如温度、压力、尺寸等),利用控制图、过程能力指数(Cp/Cpk)等工具,动态识别由设备异常、材料波动或操作偏差等特殊原因导致的系统性变异,从而实现以下目标:
- 主动预防:在质量缺陷发生前介入,减少事后检验依赖;
- 过程稳定:通过调整工艺参数或设备维护,使生产过程仅受制于无法消除的随机性波动;
- 效能提升:优化资源配置,降低不良品率及生产成本;
- 决策支持:为持续改进提供量化依据。
2.SPC关键工具
2.1样本分布图
样本分布图可通过散点形式展示数据分布,观察数据点的分散情况、密度和异常值。
样本分布图是根据设置的子组大小,X轴为子组编号,Y轴为子组对应的样本值来绘制的。从图中可观察以下内容:
- 识别异常值:散点图中远离其他子组的孤立点可能为异常值;
- 监控过程稳定性:子组内数据点集中 → 随机变异占主导,过程稳定;子组间数据分散 → 存在系统性干扰(如设备磨损、原料批次差异)需排查。
2.2正态概率图
正态概率图可验证数据是否符合正态分布,通过散点与理论正态分布直线的拟合程度判断。
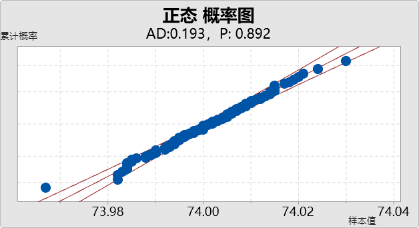
正态概率图是通过比较实际数据与理论正态分布的累积概率来绘制的。从图中可观察以下内容:
- 实际数据点
- 样本数据分布情况
- 理论曲线 (样本理论值)
- 数据点沿理论线均匀分布:说明数据正态性较好
- 置信区间曲线 (样本置信上下限)
- 样本置信上下限
- 若大部分数据点落在区间内,则认为数据符合正态分布
- 个别点超出置信区间:可能是异常值或极端值。
- 连续点系统偏离区间:提示整体分布偏离正态(如右偏、左偏或双峰分布)
- 样本置信上下限
- 正态指数
- AD
- 衡量样本数据与理论正态分布的拟合程度
- AD值越小,说明数据越接近正态分布,值越大则偏离越明显。
- P
- 衡量数据服从正态分布的概率程度
- 通常置信度是0.95,所以P值>0.05时,认为符合正态分布,反之P值≤0.05,认为偏离正态分布,
- AD
2.3控制图
控制图(Control Chart)可验证生产过程是否处于控制状态。图上有 中心线(CL)、上控制限(UCL)和下控制限(LCL),并有按时间顺序抽取的样本统计量数值的描点序列。若数据点落在两条控制界限之间且排列无缺陷,则表明生产过程正常,过程处于控制状态,否则表明生产条件发生异常,需要对过程采取措施,加强管理,使生产过程恢复正常。
控制图类别及适用范围:
| 控制图名称 | 代号 | 子组大小 | 核心用途 | 典型场景 |
|---|---|---|---|---|
| 单值-移动极差图 | I-MR图 | n=1 | 监控单值及短期变异 | 实时监控 |
| 均值-极差图 | Xbar-R图 | 2≤n≤8 | 观察均值偏移和组内极差变异 | 常规批次生产 |
| 均值-标准差图 | Xbar-S图 | n≥9 | 高精度分析均值与组内标准差变异 | 精密制造 |
I-MR图
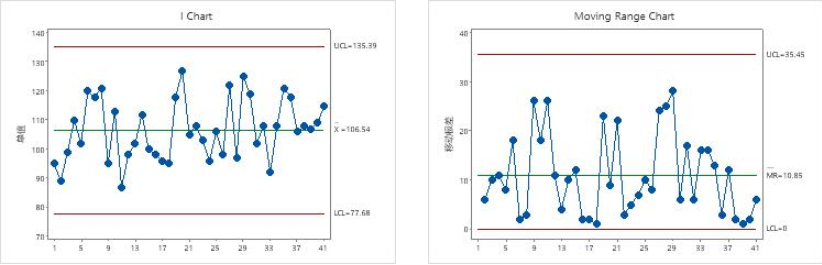
定义与用途:
- I图:直接绘制每个独立测量值(单值),适用于无法分组或样本量固定为1(n=1)的场景。例如,破坏性测试(如材料强度检测)或连续生产过程无法中断取样的情况。
- MR图:计算相邻两个单值的移动极差(即差值绝对值),用于监控单值数据中短期的变异程度,常与I图联合使用。
适用场景:
- 子组无法合理分组(如每小时只能取一个样本);
- 数据稀缺或测试成本高,难以频繁取样;
- 需快速反应过程变化(如实时监控设备参数)。
示例场景:
- 化工反应温度实时监测,每分钟记录一次数据
- 选型:I-MR图(单值连续监控,移动极差反映温度波动)
局限性:对过程变异的敏感性较低,可能掩盖微小波动
Xbar-R图
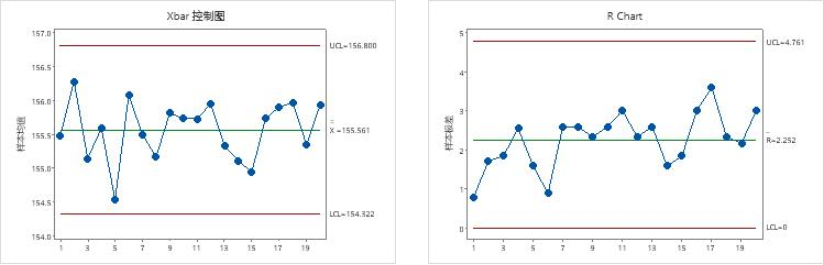
定义与用途:
- Xbar图:基于子组均值(如每组5个样本的平均值),反映过程中心位置的稳定性。适用于子组样本量较小(通常n=2-10)的情况。
- R图:计算子组内极差(最大值-最小值),监控子组内变异,常用于小样本量场景。
适用场景:
- 常规批量生产,可定期抽取子组(如每批次抽5件);
- 需要同时观察均值偏移和组内变异(如罐装工序的重量控制);
- 数据计��算简便,适合人工或快速分析。
示例场景:
- 某洗衣液工厂需监控罐装重量,每批次抽取5瓶测量
- 选型:Xbar-R图(均值反映灌装精度,极差反映组内波动)
局限性:当子组样本量较大(n≥8)时,R图对变异的估计效率较低,需改用标准差图(S图)
Xbar-S图
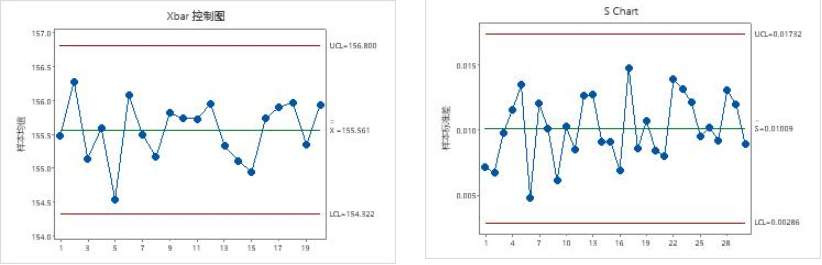
定义与用途:
- 计算子组标准差,替代R图以更精确地估计变异,尤其适用于大样本量(n≥10)。
- 与Xbar图联合使用(Xbar-S图),适用于高精度要求的场景(如半导体制造)。
适用场景:
- 子组样本量较大,需提高变异分析的准确性。
示例场景:
- 半导体晶圆缺陷检测,每小时抽取15片分析
- 选型:Xbar-S图(大样本需精确标准差分析)
局限性:计算复杂度较高,需依赖统计软件资源。
2.4运行图
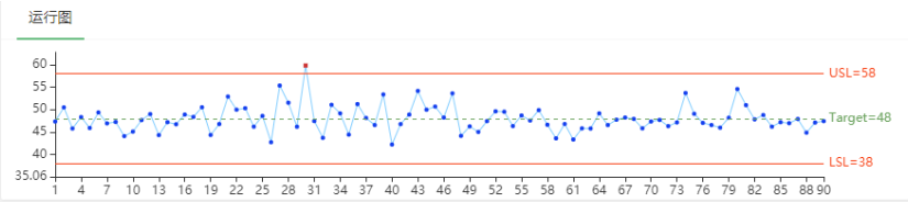
运行图(Run Chart)适用于简单趋势��跟踪和规格符合性初步判断。支持手动设置规格上下限(USL/LSL)和目标值(Target Value)作为参考线:
- 规格限:由客户或设计要求设定的合格范围,例如“零件长度10mm±0.2mm”中,USL=10.2mm,LSL=9.8mm
- 目标值:代表过程或产品的理想状态(如设计值),通常作为数据波动的基准参考
2.5过程能力图
能力直方图
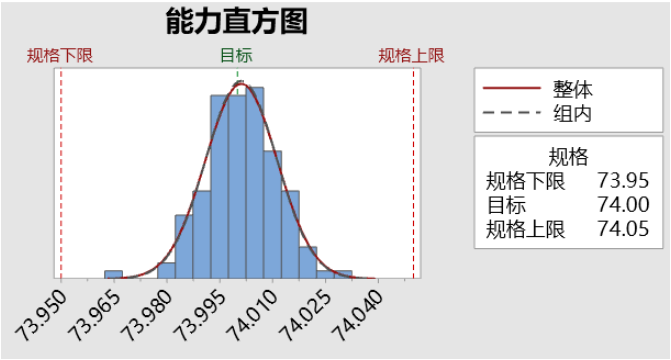
能力直方图是一种通过数据分布形态评估生产过程稳定性和能力的关键工具。通过将收集到的质量数据(如尺寸、重量等)按区间分组,以柱形高度表示各区间内的数据频数或频率,直观展示数据分布形态(如正态分布、偏态等)。通常结合过程能力分析(如Cp/Cpk指标),用于判断生产过程是否稳定、是否符合规格要求,并量化其满足质量标准的潜力
用途:
- 评估过程稳定性与能力
- 通过观察直方图的分布形态(如正态性、偏移或异常峰态),判断生产过程是否处于统计控制状态,并计算过程能力指数(如Cp、Cpk),确定工序是否具备满足公差要求的能力。例如,若直方图呈正态分布且中心与规格中心重合,表明工序能力充分;若分布偏移或分散,则需改进工艺。
- 识别质量波动与异常原因
- 直方图能直观显示质量数据的离散程度,帮助识别异常波动模式,例如:双峰型:可能混入不同生产批次或设备的数据; 锯齿型:测量误差或数据分组不当; 偏态型:刀具磨损、操作者疲劳等渐进性因素。
- 预测不合格率与改进方向
- 结合规格限(USL/LSL),通过直方图分布范围与公差范围的对比,估算潜在的不合格品率。例如,若数据分布超出规格限,需调整工艺参数或优化设备精度。
能力区间图
能力区间图是一种通过绘制控制限(组内/整体)或规格限区间,分析生产过程波动来源和稳定性的关键工具。根据范围不同分为三类:
- 组内区间图:基于子组内变差(如极差R或标准差σ),绘制控制限(如X-bar图的UCL/LCL),反映短期波动(如设备固有误差),识别特殊原因(如刀具突发磨损)。
- 整体区间图:基于全部数据的整体变差(如长期标准差),用于评估过程长期稳定性(如设备老化、环境变化),计算长期能力指数(Pp、Ppk)。
- 规格区间图:直接标注客户要求的规格限(USL/LSL),对比过程实际输出范围与客户需求,判断是否符合标准。
2.6过程能力指标
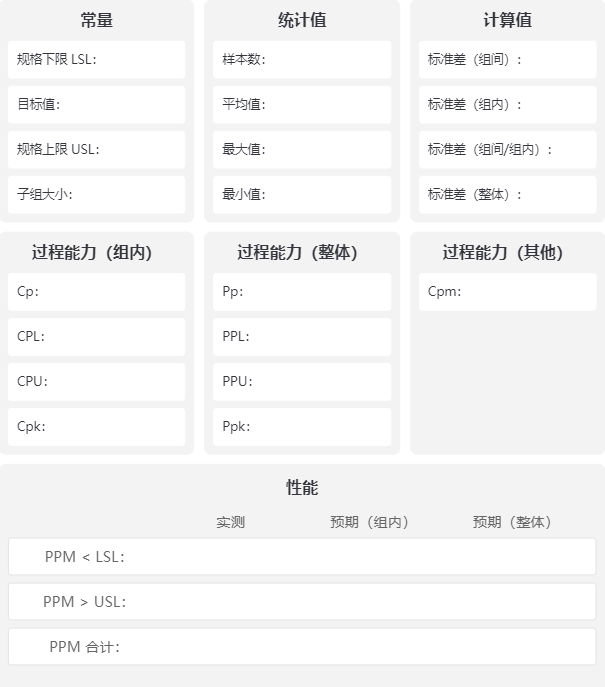
①指标说明
- 过程能力(组内)
| 指标名称 | 指标含义 | 指标说明 |
|---|---|---|
| Ca | 过程准确度 | 衡量过程均值与目标值的偏移程度,可以理解为“中心偏移程度”,范围:0(无偏移)~1(完全偏离) |
| Cp | 潜在过程能力指数 | 不考虑过程的偏移(仅衡量组内�波动),可以理解为“过程的潜在能力或最高水平“ |
| CPL | 下限过程能力指数 | 衡量过程均值与规格下限的距离,可以理解为“下限合格能力” |
| CPU | 上限过程能力指数 | 衡量过程均值与规格上限的距离,可以理解为“上限限合格能力” |
| CPK | 实际过程能力指数 | 同时考虑组内波动和过程的偏移,可以理解为“过程的实际能力或合格率” |
| PPM | 潜在百万分之缺陷数 | 能力指数推算的理论缺陷数,可以理解为“质量风险水平” |
- 过程能力(整体)
| 指标名称 | 指标含义 | 指标说明 |
|---|---|---|
| Pp | 潜在过程绩效指数 | 从过程总波动(组内+组间)角度考察潜在过程能力,包含随机和非随机因素影响 |
| PPL | 下限过程绩效指数 | 长期数据下的下限能力评估 |
| PPU | 上限过程绩效指数 | 长期数据下的上限能力评估 |
| PpK | 实际过程绩效指数 | 从过程总波动(组内+组间)角度考察实际过程能力,同时考虑均值偏移和随机/非随机因素影响 |
| PPM | 潜在百万分之缺陷数 | 能力指数推算的理论缺陷数,可以理解为“质量风险水平” |
- 过程能力(其他)
| 指标名称 | 指标含义 | 指标说明 |
|---|---|---|
| Cpm | 第二代过程能力指数 | 考虑过程均值与目标值的偏差,反映优等品率 |
②Cpk评价参考
| Cpk值的范围 | 级别 | 评价 | 改进措施 |
|---|---|---|---|
| Cpk ≥ 1.67 | A+ | 过程能力过于充足 | 降低费用,减少成本 |
| 1.67 > Cpk ≥ 1.33 | A | 过程能力充足 | 维持现状 |
| 1.33 > Cpk ≥ 1.00 | B | 过程能力尚可 | 应设法提高为A级 |
| 1.00 > Cpk ≥ 0.67 | C | 过程能力不足 | 应采取措施,立即改善 |
| 0.67 > Cpk | D | 过程能力严重不足 | 采取紧急措施和全面检查,必要时停工整顿 |
3.组态SPC分析页面
3.1数据采样
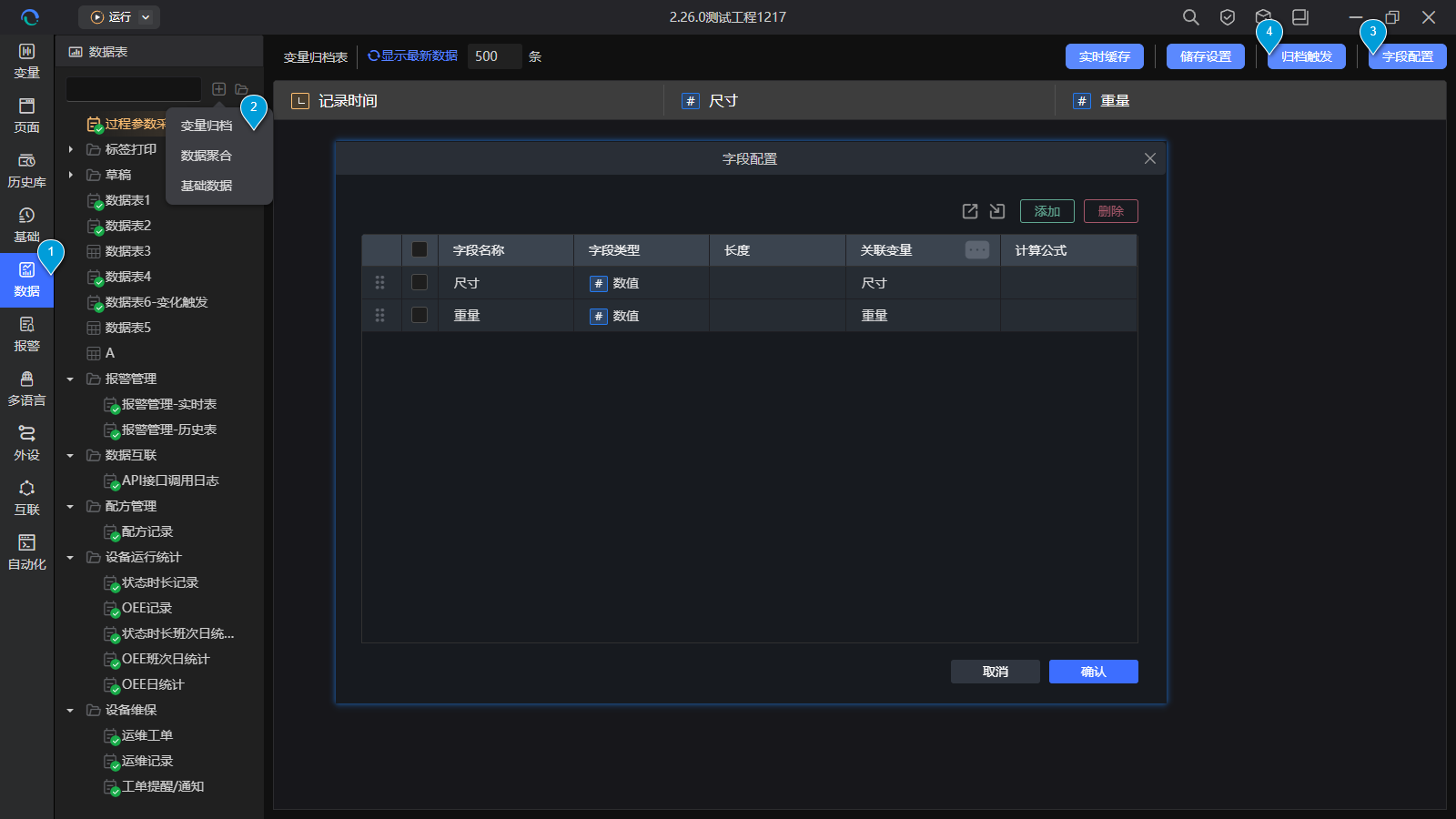
将关键质量参数(如尺寸、重量等)进行数据归档。
操作如下:打开【数据管理】,创建【数据归档表】,关联变量字段,设置数据采样规则(如定时)
3.2报告搭建
根据分析需要,拖拽对应的统计图和能力指标至画布中,即可搭建SPC分析画面。
操作如下:
①选用组件:
| 关键工具 | 图表类型 | |
|---|---|---|
| 样本分布图 | 选用散点图-SPC类型-样本分布图 | |
| 正态概率图 | 选用散点图-SPC类型-正态概率图 | |
| 控制图 | 选用折线图-SPC类型-控制图 | |
| 运行图 | 选用折线图-SPC类型-运行图 | |
| 能力直方图 | 选用组合图-SPC类型-能力直方图 | |
| 能力区间图 | 选用区间图-SPC类型-能力区间图 | |
| 能力指标 | 选用能力图后,将能力指标结果输出至变量,使用数值显示组件展示对应的能力指标 |
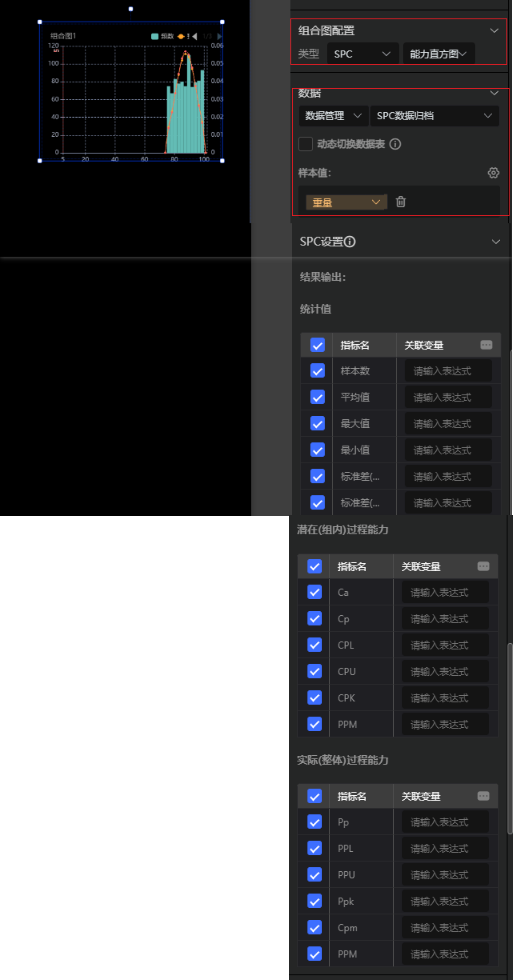
②配置数据:关联数据采集表,选择需要分析的参数
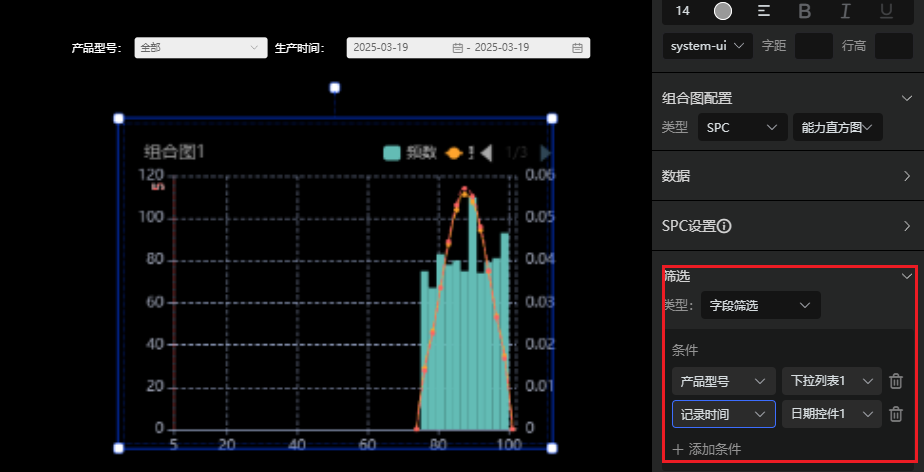
3.3选择样本
通过图表数据筛选样本数据,如某时段、某批次等数据。
操作如下:
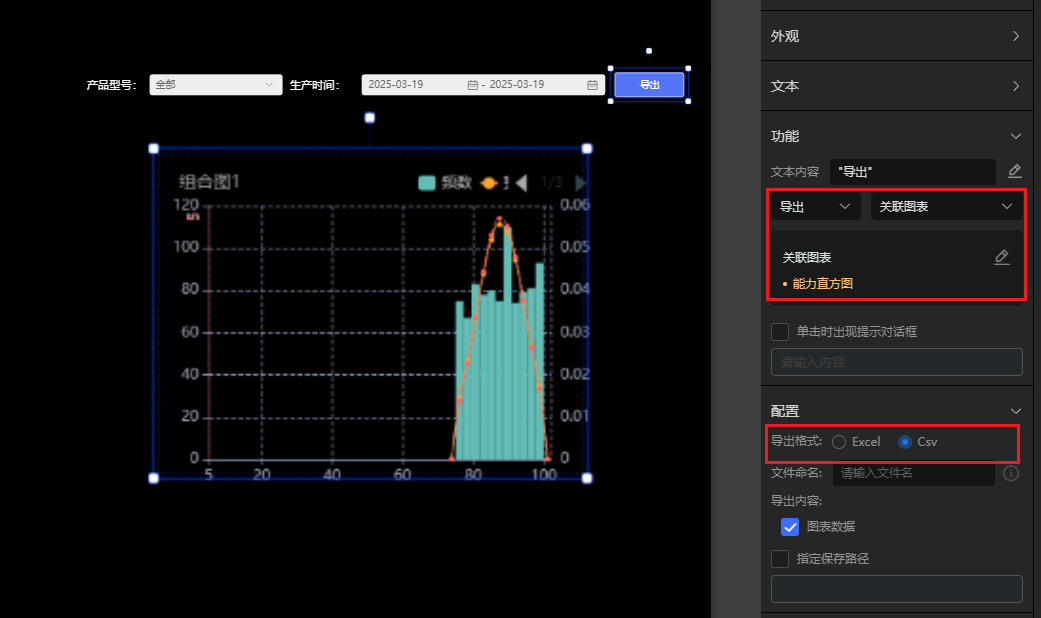
3.4报告导出
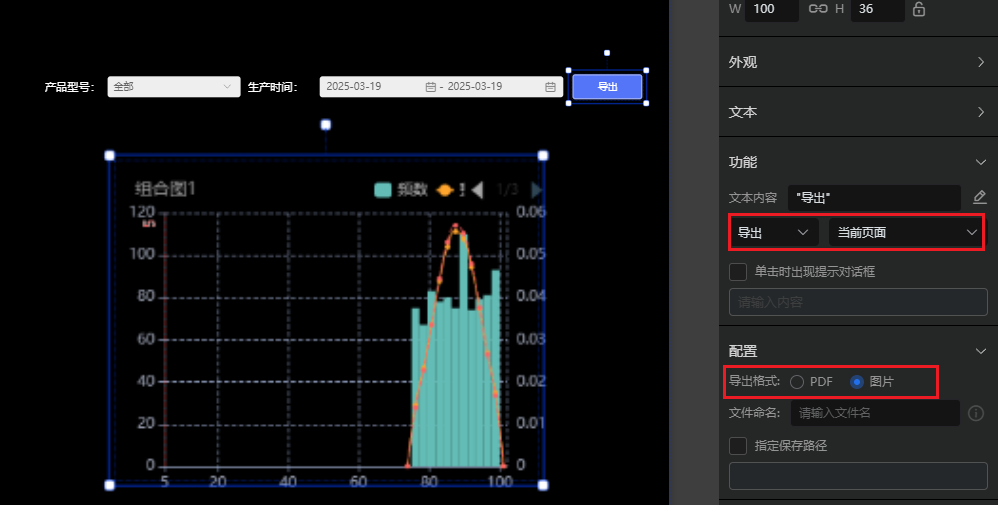
通过导出功能,可导出报告,进行归档。
导出报告图片:
导出样本数据: